We consider a variant of the game of Cops and Robbers, called Lazy Cops and Robbers, where at most one cop can move in any round. We investigate the analogue of the cop number for this game, which we call the lazy cop number. Lazy Cops and Robbers was recently introduced by Offner and Ojakian, who provided asymptotic upper and lower bounds on the lazy cop number of the hypercube. By coupling the probabilistic method with a potential function argument, we improve on the existing lower bounds for the lazy cop number of hypercubes.

Cops and robbers is a turn-based pursuit game played on a graph G. One robber is pursued by a set of cops. In each round, these agents move between vertices along the edges of the graph. The cop number c(G) denotes the minimum number of cops required to catch the robber in finite time. We study the cop number of geometric graphs. For points x1, . . ., xn ∈ ℝ2, and r ∈ ℝ+, the vertex set of the geometric graph G(x1, . . ., xn; r) is the graph on these n points, with xi, xj adjacent when ∥xi − xj∥ ≤ r. We prove that c(G) ≤ 9 for any connected geometric graph G in ℝ2 and we give an example of a connected geometric graph with c(G) = 3. We improve on our upper bound for random geometric graphs that are sufficiently dense. Let 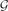(n,r) denote the probability space of geometric graphs with n vertices chosen uniformly and independently from [0,1]2. For G ∈ 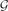(n,r), we show that with high probability (w.h.p.), if r ≥ K1 (log n/n)1/4 then c(G) ≤ 2, and if r ≥ K2(log n/n)1/5 then c(G) = 1, where K1, K2 > 0 are absolute constants. Finally, we provide a lower bound near the connectivity regime of 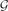(n,r): if r ≤ K3 log n/ 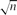then c(G) > 1 w.h.p., where K3 > 0 is an absolute constant.