1 results
On (Not) Computing the Möbius Function Using Bounded Depth Circuits
-
- Journal:
- Combinatorics, Probability and Computing / Volume 21 / Issue 6 / November 2012
- Published online by Cambridge University Press:
- 24 August 2012, pp. 942-951
-
- Article
- Export citation
-
Any function F: {0,. . ., N − 1} → {−1,1} such that F(x) can be computed from the binary digits of x using a bounded depth circuit is orthogonal to the Möbius function μ in the sense that
The proof combines a result of Linial, Mansour and Nisan with techniques of Kátai and Harman, used in their work on finding primes with specified digits.
\[
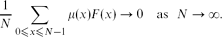\frac{1}{N} \sum_{0 \leq x \leq N-1} \mu(x)F(x) → 0 \quad\text{as}~~ N → \infty.
\]
