In present paper we define a new kind of quantized enveloping algebra of 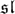 (2). We denote this algebra by Ur,t, where r, t are two non-negative integers. It is a non-commutative and non-cocommutative Hopf algebra. If r = 0, then the algebra Ur,t is isomorphic to a tensor product of the algebra of infinite cyclic group and the usual quantum enveloping algebra of
(2). We denote this algebra by Ur,t, where r, t are two non-negative integers. It is a non-commutative and non-cocommutative Hopf algebra. If r = 0, then the algebra Ur,t is isomorphic to a tensor product of the algebra of infinite cyclic group and the usual quantum enveloping algebra of 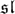 (2) as Hopf algebras. The representation of this algebra is studied.
(2) as Hopf algebras. The representation of this algebra is studied.
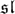 (2)
(2)