We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let P - {p1,p2,. . . ,pn} be an independent point-set in ℝd (i.e., there are no d + 1 on a hyperplane). A simplex determined by d + 1 different points of P is called empty if it contains no point of P in its interior. Denote the number of empty simplices in P by fd(P). Katchalski and Meir pointed out that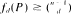 
. Here a random construction Pn is given with 
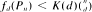, where K(d) is a constant depending only on d. Several related questions are investigated.
