We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The geography and botany problems of irreducible non-spin symplectic 4-manifolds with a choice of fundamental group from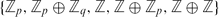 
$\{{\mathbb{Z}}_p, {\mathbb{Z}}_p\oplus {\mathbb{Z}}_q, {\mathbb{Z}}, {\mathbb{Z}}\oplus {\mathbb{Z}}_p, {\mathbb{Z}}\oplus {\mathbb{Z}}\}$ are studied by building upon the recent progress obtained on the simply connected realm. Results on the botany of simply connected 4-manifolds not available in the literature are extended.
