1 results
Projective invariants of images
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 936-946
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
The method of equivariant moving frames is employed to construct and completely classify the differential invariants for the action of the projective group on functions defined on the two-dimensional projective plane. While there are four independent differential invariants of order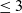
$\leq 3$, it is proved that the algebra of differential invariants is generated by just two of them through invariant differentiation. The projective differential invariants are, in particular, of importance in image processing applications.
