We solve a problem proposed by V. Klee (1969). He asked for a calculation of κ, the expected value of V, the volume of a daughter tetrahedron whose vertices are chosen at random (i.e. independently and uniformly) in the interior of a parent tetrahedron of unit volume. We discover: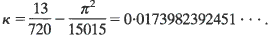
We also calculate the second, fourth and sixth moments of V.