We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Two arbitrary life distributions F and G can be ordered with respect to their Laplace transforms. We say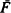 
is Laplace-smaller than 
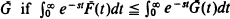for all s > 0. Interpretations of this ordering concept in reliability, operations research, and economics are described. General preservation properties are presented. Using these preservation results we derive useful inequalities and discuss their applications to M/G/1 queues, time series, coherent systems, shock models and cumulative damage models.
