The paper considers a modified storage process with state space [0,∞). Away from the origin, W behaves like an ordinary storage process with constant release rate and finite jump intensity A. In state 0, however, the jump intensity falls to It is shown that W can be obtained by applying first a reflection mapping and then a random change of time scale to a compound Poisson process with drift. When these same two transformations are applied to Brownian motion, one obtains sticky (or slowly reflected) Brownian motion W∗ on [0,∞). Thus W∗ is the natural diffusion approximation for W, and it is shown that W converges in distribution to W∗ under appropriate conditions. The boundary behavior of W∗ is discussed, its infinitesimal generator is calculated and its stationary distribution (which has an atom at the origin) is computed.

For correlated random walks a method of transition probability matrices as an alternative to the much-used methods of probability generating functions and difference equations has been investigated in this paper. To illustrate the use of transition probability matrices for computing the various probabilities for correlated random walks, the transition probability matrices for restricted/unrestricted one-dimensional correlated random walk have been defined and used to obtain some of the probabilities.

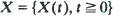Let be a process with stationary, independent increments and no negative jumps. Let 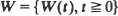be this same process modified by a reflecting barrier at zero (a storage process). Assuming that – 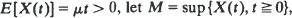and denote by ψ(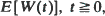s) the exponent function of X. A simple formula is derived for the Laplace transform of as a function of 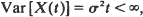W(0). Using the fact that the distribution of M is the unique stationary distribution of the Markov process W, this yields an elementary proof that the Laplace transform of M is µs/ψ(s). If it follows that 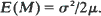These surprisingly simple formulas were originally obtained by Zolotarev using analytical methods.