A martingale is used to study extinction probabilities of the Galton-Watson process using a stopping time argument. This same martingale defines a martingale function in its argument s; consequently, its derivative is also a martingale. The argument s can be classified as regular or irregular and this classification dictates very different behavior of the Galton-Watson process. For example, it is shown that irregularity of a point s is equivalent to the derivative martingale sequence at s being closable, (i.e., it has limit which, when attached to the original sequence, the martingale structure is retained). It is also shown that for irregular points the limit of the derivative is the derivative of the limit, and two different types of norming constants for the asymptotics of the Galton-Watson process are asymptotically equivalent only for irregular points.

It is shown that the limiting random variable W(si) of an irregular branching process with infinite mean, defined in [5], has a continuous and positive distribution on {0 < W(si) < ∞}. This implies that for all branching processes (Zn) with infinite mean there exists a function U such that the distribution of V = limnU(Zn)e–n a.s. is continuous, positive and finite on the set of non-extinction. A kind of law of large numbers for sequences of independent copies of W(si) is derived.

The paper deals with the asymptotic behaviour of infinite mean Galton–Watson processes (denoted by {Zn}). We show that these processes can be classified as regular or irregular. The regular ones are characterized by the property that for any sequence of positive constants {Cn}, for which 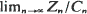a.s. exists, 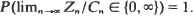The irregular ones, which will be shown by examples to exist, have the property that there exists a sequence of constants {Cn} such that 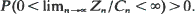In Part 1 we study the properties of {Zn/Cn} and give some characterizations for both regular and irregular processes. Part 2 starts with an a.s. convergence result for {yn(Zn)}, where {yn} is a suitable chosen sequence of functions related to {Zn}. Using this, we then derive necessary and sufficient conditions for the a.s. convergence of {U(Zn)/Cn}, where U is a slowly varying function. The distribution function of the limit is shown to satisfy a Poincaré functional equation. Finally we show that for every process {Zn} it is possible to construct explicitly functions U, such that U(Zn)/en converges a.s. to a non-degenerate proper random variable. If the process is regular, all these functions U are slowly varying. The distribution of the limit depends on U, and we show that by appropriate choice of U we may get a limit distribution which has a positive and continuous density or is continuous but not absolutely continuous or even has no probability mass on certain intervals. This situation contrasts strongly with the finite mean case.