1 results
The substability and ergodicity of complicated queueing systems
-
- Journal:
- Journal of Applied Probability / Volume 23 / Issue 1 / March 1986
- Published online by Cambridge University Press:
- 14 July 2016, pp. 193-200
- Print publication:
- March 1986
-
- Article
- Export citation
-
The substability and the ergodicity of various queueing models are discussed. This paper considers the vector-valued queueing process Xrn = (xrn,1,xrn,2, · ··) with non-negative components and a constant initial value Xrr= a. For this, the substability is derived under simple conditions by showing the finiteness of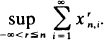
With respect to the ergodicity, in order to make use of Borovkov's theorem, we additionally assume that the distribution of the interarrival of customers has non-bounded tail for any given past sequence.
