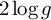In this note we show that the expected value of the separating systole of a random surface of genus g with respect to Weil–Petersson volume behaves like $2\log g $ as the genus goes to infinity. This is in strong contrast to the behavior of the expected value of the systole which, by results of Mirzakhani and Petri, is independent of genus.

We study the sample path properties of χ2 random surfaces, in particular in the neighbourhood of their extrema. We show that, as is the case for their Gaussian counterparts, χ2 surfaces at high levels follow the form of certain deterministic paraboloids, but that, unlike their Gaussian counterparts, at low levels their form is much more random. This has a number of interesting implications in the modelling of rough surfaces and the study of the ‘robustness' of Gaussian field models. The general approach of the paper is the study of extrema via the ‘Slepian model process', which, for χ2 fields, is tractable only at asymptotically high or low levels.