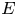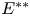1 results
Order continuity of Arens extensions of regular multilinear operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 September 2023, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
-
First we give a counterexample showing that recent results on separate order continuity of Arens extensions of multilinear operators cannot be improved to get separate order continuity on the product of the whole of the biduals. Then we establish conditions on the operators and/or on the underlying Riesz spaces/Banach lattices so that the extensions are order continuous on the product of the whole biduals. We also prove that all Arens extensions of any regular multilinear operator are order continuous in at least one variable and we study when Arens extensions of regular homogeneous polynomials on a Banach lattice $E$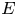
are order continuous on $E^{**}$
.
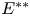