We study the noise sensitivity of the minimum spanning tree (MST) of the $n$-vertex complete graph when edges are assigned independent random weights. It is known that when the graph distance is rescaled by $n^{1/3}$ and vertices are given a uniform measure, the MST converges in distribution in the Gromov–Hausdorff–Prokhorov (GHP) topology. We prove that if the weight of each edge is resampled independently with probability $\varepsilon \gg n^{-1/3}$, then the pair of rescaled minimum spanning trees – before and after the noise – converges in distribution to independent random spaces. Conversely, if $\varepsilon \ll n^{-1/3}$, the GHP distance between the rescaled trees goes to $0$ in probability. This implies the noise sensitivity and stability for every property of the MST that corresponds to a continuity set of the random limit. The noise threshold of $n^{-1/3}$ coincides with the critical window of the Erdős-Rényi random graphs. In fact, these results follow from an analog theorem we prove regarding the minimum spanning forest of critical random graphs.

We investigate random minimal factorizations of the n-cycle, that is, factorizations of the permutation 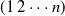$(1 \, 2 \cdots n)$ into a product of cycles 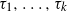$\tau_1, \ldots, \tau_k$ whose lengths 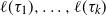$\ell(\tau_1), \ldots, \ell(\tau_k)$ satisfy the minimality condition 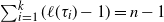$\sum_{i=1}^k(\ell(\tau_i)-1)=n-1$ . By associating to a cycle of the factorization a black polygon inscribed in the unit disk, and reading the cycles one after another, we code a minimal factorization by a process of colored laminations of the disk. These new objects are compact subsets made of red noncrossing chords delimiting faces that are either black or white. Our main result is the convergence of this process as 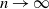$n \rightarrow \infty$ , when the factorization is randomly chosen according to Boltzmann weights in the domain of attraction of an $\alpha$ -stable law, for some 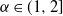$\alpha \in (1,2]$ . The limiting process interpolates between the unit circle and a colored version of Kortchemski’s $\alpha$ -stable lamination. Our principal tool in the study of this process is a new bijection between minimal factorizations and a model of size-conditioned labeled random trees whose vertices are colored black or white, as well as the investigation of the asymptotic properties of these trees.

A pair of bouncing geometric Brownian motions (GBMs) is studied. The bouncing GBMs behave like GBMs except that, when they meet, they bounce off away from each other. The object of interest is the position process, which is defined as the position of the latest meeting point at each time. We study the distributions of the time and position of their meeting points, and show that the suitably scaled logarithmic position process converges weakly to a standard Brownian motion as the bounce size δ→0. We also establish the convergence of the bouncing GBMs to mutually reflected GBMs as δ→0. Finally, applying our model to limit order books, we derive a simple and effective prediction formula for trading prices.

We study a multistage epidemic model which generalizes the SIR model and where infected individuals go through K ≥ 1 stages of the epidemic before being removed. An infected individual in stage k ∈ {1, …, K} may infect a susceptible individual, who directly goes to stage k of the epidemic; or it may go to the next stage k + 1 of the epidemic. For this model, we identify the critical regime in which we establish diffusion approximations. Surprisingly, the limiting diffusion exhibits an unusual form of state space collapse which we analyze in detail.

We analyse the queue QL at a multiplexer with L sources which may display long-range dependence. This includes, for example, sources modelled by fractional Brownian motion (FBM). The workload processes W due to each source are assumed to have large deviation properties of the form P[Wt/a(t) > x] ≈ exp[– v(t)K(x)] for appropriate scaling functions a and v, and rate-function K. Under very general conditions limL→xL–1 log P[QL > Lb] = – I(b), provided the offered load is held constant, where the shape function I is expressed in terms of the cumulant generating functions of the input traffic. For power-law scalings v(t) = tv, a(t) = ta (such as occur in FBM) we analyse the asymptotics of the shape function limb→xb–u/a(I(b) – δbv/a) = vu for some exponent u and constant v depending on the sources. This demonstrates the economies of scale available though the multiplexing of a large number of such sources, by comparison with a simple approximation P[QL > Lb] ≈ exp[−δLbv/a] based on the asymptotic decay rate δ alone. We apply this formula to Gaussian processes, in particular FBM, both alone, and also perturbed by an Ornstein–Uhlenbeck process. This demonstrates a richer potential structure than occurs for sources with linear large deviation scalings.