We prove that for a vast class of random walks on a compactly generated group, the exponential growth of convolutions of a probability density function along almost every sample path is bounded by the growth of the group. As an application, we show that the almost sure and 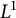 $L^1$ convergences of the Shannon–McMillan–Breiman theorem hold for compactly supported random walks on compactly generated groups with subexponential growth.
$L^1$ convergences of the Shannon–McMillan–Breiman theorem hold for compactly supported random walks on compactly generated groups with subexponential growth.