1 results
The geometry of random drift I. Stochastic distance and diffusion
-
- Journal:
- Advances in Applied Probability / Volume 9 / Issue 2 / June 1977
- Published online by Cambridge University Press:
- 01 July 2016, pp. 238-249
- Print publication:
- June 1977
-
- Article
- Export citation
-
A stochastic distance measure is defined for a general diffusion process on a parameter space X. This distance is defined by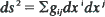
where (gij) is the inverse of the covariance matrix of the diffusion equation. This permits the study of the geometry associated with a diffusion equation, since the matrix (gij) is the fundamental tensor of the Riemannian space (X, gij), and of a diffusion process in terms of Brownian motion. For the diffusion equation approximation to random drift with n alleles the covariance matrix is that of a multinomial distribution. The resulting stochastic distance is equal to twice the genetic distance as defined by Cavalli-Sforza and Edwards and is a generalization of the angular transformation of Fisher to n alleles. The geometry associated with the diffusion equation for random drift with n alleles is that of a 
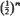part of an (n − 1)-sphere of radius two. We also show that the diffusion equation for random drift is not spherical Brownian motion, although it is approximated by it near the centroid of frequency space.
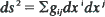where (
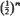part of an (