1 results
Sandwiched SDEs with unbounded drift driven by Hölder noises
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 08 March 2023, pp. 927-964
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
We study a stochastic differential equation with an unbounded drift and general Hölder continuous noise of order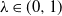
$\lambda \in (0,1)$. The corresponding equation turns out to have a unique solution that, depending on a particular shape of the drift, either stays above some continuous function or has continuous upper and lower bounds. Under some mild assumptions on the noise, we prove that the solution has moments of all orders. In addition, we provide its connection to the solution of some Skorokhod reflection problem. As an illustration of our results and motivation for applications, we also suggest two stochastic volatility models which we regard as generalizations of the CIR and CEV processes. We complete the study by providing a numerical scheme for the solution.
