We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let n=2,3,4,5 and let X be a smooth complex projective hypersurface of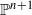 
. In this paper we find an effective lower bound for the degree of X, such that every holomorphic entire curve in X must satisfy an algebraic differential equation of order k=n=dim X, and also similar bounds for order k>n. Moreover, for every integer n≥2, we show that there are no such algebraic differential equations of order k<n for a smooth hypersurface in .
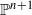