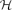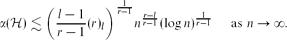Search

A partial Steiner (n,r,l)-system is an r-uniform hypergraph on n vertices in which every set of l vertices is contained in at most one edge. A partial Steiner (n,r,l)-system is complete if every set of l vertices is contained in exactly one edge. In a hypergraph 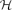, the independence number α(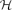) denotes the maximum size of a set of vertices in 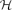containing no edge. In this article we prove the following. Given integers r,l such that r ≥ 2l − 1 ≥ 3, we prove that there exists a partial Steiner (n,r,l)-system 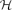such that

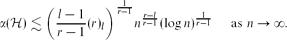$$\alpha(\HH) \lesssim \biggl(\frac{l-1}{r-1}(r)_l\biggr)^{\frac{1}{r-1}}n^{\frac{r-l}{r-1}} (\log n)^{\frac{1}{r-1}} \quad \mbox{ as }n \rightarrow \infty.$$

This improves earlier results of Phelps and Rödl, and Rödl and Ŝinajová. We conjecture that it is best possible as it matches the independence number of a random r-uniform hypergraph of the same density. If l = 2 or l = 3, then for infinitely many r the partial Steiner systems constructed are complete for infinitely many n.

Search Results

Refine search

Refine search

Actions for selected content:

1 results

On the Independence Number of Steiner Systems

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

1 results

On the Independence Number of Steiner Systems