2 results
A NOTE ON WEIGHTED BADLY APPROXIMABLE LINEAR FORMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 349-357
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
A NOTE ON SIMULTANEOUS AND MULTIPLICATIVE DIOPHANTINE APPROXIMATION ON PLANAR CURVES
-
- Journal:
- Glasgow Mathematical Journal / Volume 49 / Issue 2 / May 2007
- Published online by Cambridge University Press:
- 09 August 2007, pp. 367-375
- Print publication:
- May 2007
-
- Article
-
- You have access
- Export citation
-
Let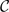
be a non-degenerate planar curve. We show that the curve is of Khintchine-type for convergence in the case of simultaneous approximation in 
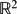with two independent approximation functions; that is if a certain sum converges then the set of all points (x,y) on the curve which satisfy simultaneously the inequalities ||qx|| < ψ1(q) and ||qy|| < ψ2(q) infinitely often has induced measure 0. This completes the metric theory for the Lebesgue case. Further, for multiplicative approximation ||qx|| ||qy|| < ψ(q) we establish a Hausdorff measure convergence result for the same class of curves, the first such result for a general class of manifolds in this particular setup.
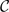be a non-degenerate planar curve. We show that the curve is of Khintchine-type for convergence in the case of simultaneous approximation in 
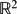with two independent approximation functions; that is if a certain sum converges then the set of all points (