Let I be a set and let 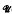 (I) denote the set consisting of the 0 matrix over I × I and the matrix units over I × I. Then for x, z in
(I) denote the set consisting of the 0 matrix over I × I and the matrix units over I × I. Then for x, z in 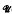 (I) and x≠0≠z, xyz≠0 has precisely one solution y. This and several other statements are shown to be equivalent characterizations of
(I) and x≠0≠z, xyz≠0 has precisely one solution y. This and several other statements are shown to be equivalent characterizations of 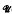 (I) regarded as a semigroup with zero.
(I) regarded as a semigroup with zero.
1980 Mathematics subject classification (Amer. Math. Soc.): 20 M 10.