1 results
SHAPIRO’S UNCERTAINTY PRINCIPLE IN THE DUNKL SETTING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 29 April 2015, pp. 98-110
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
-
The Dunkl transform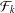
${\mathcal{F}}_{k}$ is a generalisation of the usual Fourier transform to an integral transform invariant under a finite reflection group. The goal of this paper is to prove a strong uncertainty principle for orthonormal bases in the Dunkl setting which states that the product of generalised dispersions cannot be bounded for an orthonormal basis. Moreover, we obtain a quantitative version of Shapiro’s uncertainty principle on the time–frequency concentration of orthonormal sequences and show, in particular, that if the elements of an orthonormal sequence and their Dunkl transforms have uniformly bounded dispersions then the sequence is finite.
