This paper is concerned with the relationship of $y$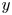 -smooth integers and de Bruijn's approximation $\Lambda (x,\,y)$
-smooth integers and de Bruijn's approximation $\Lambda (x,\,y)$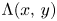 . Under the Riemann hypothesis, Saias proved that the count of $y$
. Under the Riemann hypothesis, Saias proved that the count of $y$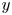 -smooth integers up to $x$
-smooth integers up to $x$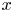 , $\Psi (x,\,y)$
, $\Psi (x,\,y)$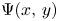 , is asymptotic to $\Lambda (x,\,y)$
, is asymptotic to $\Lambda (x,\,y)$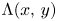 when $y \ge (\log x)^{2+\varepsilon }$
when $y \ge (\log x)^{2+\varepsilon }$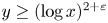 . We extend the range to $y \ge (\log x)^{3/2+\varepsilon }$
. We extend the range to $y \ge (\log x)^{3/2+\varepsilon }$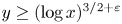 by introducing a correction factor that takes into account the contributions of zeta zeros and prime powers. We use this correction term to uncover a lower order term in the asymptotics of $\Psi (x,\,y)/\Lambda (x,\,y)$
by introducing a correction factor that takes into account the contributions of zeta zeros and prime powers. We use this correction term to uncover a lower order term in the asymptotics of $\Psi (x,\,y)/\Lambda (x,\,y)$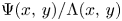 . The term relates to the error term in the prime number theorem, and implies that large positive (resp. negative) values of $\sum _{n \le y} \Lambda (n)-y$
. The term relates to the error term in the prime number theorem, and implies that large positive (resp. negative) values of $\sum _{n \le y} \Lambda (n)-y$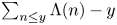 lead to large positive (resp. negative) values of $\Psi (x,\,y)-\Lambda (x,\,y)$
lead to large positive (resp. negative) values of $\Psi (x,\,y)-\Lambda (x,\,y)$ , and vice versa. Under the Linear Independence hypothesis, we show a Chebyshev's bias in $\Psi (x,\,y)-\Lambda (x,\,y)$
, and vice versa. Under the Linear Independence hypothesis, we show a Chebyshev's bias in $\Psi (x,\,y)-\Lambda (x,\,y)$ .
.