1 results
On Steenrod 𝕃-homology, generalized manifolds, and surgery
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 20 March 2020, pp. 579-607
-
- Article
- Export citation
-
The aim of this paper is to show the importance of the Steenrod construction of homology theories for the disassembly process in surgery on a generalized n-manifold Xn, in order to produce an element of generalized homology theory, which is basic for calculations. In particular, we show how to construct an element of the nth Steenrod homology group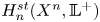
$H^{st}_{n} (X^{n}, \mathbb {L}^+)$, where 𝕃+ is the connected covering spectrum of the periodic surgery spectrum 𝕃, avoiding the use of the geometric splitting procedure, the use of which is standard in surgery on topological manifolds.
