We use Stein’s method to obtain distributional approximations of subgraph counts in the uniform attachment model or random directed acyclic graph; we provide also estimates of rates of convergence. In particular, we give uni- and multi-variate Poisson approximations to the counts of cycles and normal approximations to the counts of unicyclic subgraphs; we also give a partial result for the counts of trees. We further find a class of multicyclic graphs whose subgraph counts are a.s. bounded as $n\to \infty$.

We use Stein’s method to establish the rates of normal approximation in terms of the total variation distance for a large class of sums of score functions of samples arising from random events driven by a marked Poisson point process on $\mathbb{R}^d$. As in the study under the weaker Kolmogorov distance, the score functions are assumed to satisfy stabilisation and moment conditions. At the cost of an additional non-singularity condition, we show that the rates are in line with those under the Kolmogorov distance. We demonstrate the use of the theorems in four applications: Voronoi tessellations, k-nearest-neighbours graphs, timber volume, and maximal layers.

We study the coupon collector’s problem with group drawings. Assume there are n different coupons. At each time precisely s of the n coupons are drawn, where all choices are supposed to have equal probability. The focus lies on the fluctuations, as $n\to\infty$, of the number $Z_{n,s}(k_n)$ of coupons that have not been drawn in the first $k_n$ drawings. Using a size-biased coupling construction together with Stein’s method for normal approximation, a quantitative central limit theorem for $Z_{n,s}(k_n)$ is shown for the case that $k_n=({n/s})(\alpha\log(n)+x)$, where $0<\alpha<1$ and $x\in\mathbb{R}$. The same coupling construction is used to retrieve a quantitative Poisson limit theorem in the boundary case $\alpha=1$, again using Stein’s method.

It is well known that each statistic in the family of power divergence statistics, across n trials and r classifications with index parameter 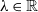$\lambda\in\mathbb{R}$ (the Pearson, likelihood ratio, and Freeman–Tukey statistics correspond to 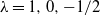$\lambda=1,0,-1/2$ , respectively), is asymptotically chi-square distributed as the sample size tends to infinity. 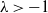We obtain explicit bounds on this distributional approximation, measured using smooth test functions, that hold for a given finite sample n, and all index parameters ( $\lambda>-1$ ) for which such finite-sample bounds are meaningful. We obtain bounds that are of the optimal order 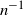$n^{-1}$ . The dependence of our bounds on the index parameter 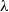$\lambda$ and the cell classification probabilities is also optimal, and the dependence on the number of cells is also respectable. Our bounds generalise, complement, and improve on recent results from the literature.

The generalized perturbative approach is an all-purpose variant of Stein’s method used to obtain rates of normal approximation. Originally developed for functions of independent random variables, this method is here extended to functions of the realization of a hidden Markov model. In this dependent setting, rates of convergence are provided in some applications, leading, in each instance, to an extra log-factor vis-à-vis the rate in the independent case.

A classical result for the simple symmetric random walk with 2n steps is that the number of steps above the origin, the time of the last visit to the origin, and the time of the maximum height all have exactly the same distribution and converge when scaled to the arcsine law. Motivated by applications in genomics, we study the distributions of these statistics for the non-Markovian random walk generated from the ascents and descents of a uniform random permutation and a Mallows(q) permutation and show that they have the same asymptotic distributions as for the simple random walk. We also give an unexpected conjecture, along with numerical evidence and a partial proof in special cases, for the result that the number of steps above the origin by step 2n for the uniform permutation generated walk has exactly the same discrete arcsine distribution as for the simple random walk, even though the other statistics for these walks have very different laws. We also give explicit error bounds to the limit theorems using Stein’s method for the arcsine distribution, as well as functional central limit theorems and a strong embedding of the Mallows(q) permutation which is of independent interest.

Explicit bounds are given for the Kolmogorov and Wasserstein distances between a mixture of normal distributions, by which we mean that the conditional distribution given some $\sigma$ -algebra is normal, and a normal distribution with properly chosen parameter values. The bounds depend only on the first two moments of the first two conditional moments given the $\sigma$ -algebra. The proof is based on Stein’s method. As an application, we consider the Yule–Ornstein–Uhlenbeck model, used in the field of phylogenetic comparative methods. We obtain bounds for both distances between the distribution of the average value of a phenotypic trait over n related species, and a normal distribution. The bounds imply and extend earlier limit theorems by Bartoszek and Sagitov.

We study a class of load-balancing algorithms for many-server systems (N servers). Each server has a buffer of size $b-1$ with $b=O(\sqrt{\log N})$, i.e. a server can have at most one job in service and $b-1$ jobs queued. We focus on the steady-state performance of load-balancing algorithms in the heavy traffic regime such that the load of the system is $\lambda = 1 - \gamma N^{-\alpha}$ for $0<\alpha<0.5$ and $\gamma > 0,$ which we call the sub-Halfin–Whitt regime ($\alpha=0.5$ is the so-called Halfin–Whitt regime). We establish a sufficient condition under which the probability that an incoming job is routed to an idle server is 1 asymptotically (as $N \to \infty$) at steady state. The class of load-balancing algorithms that satisfy the condition includes join-the-shortest-queue, idle-one-first, join-the-idle-queue, and power-of-d-choices with $d\geq \frac{r}{\gamma}N^\alpha\log N$ (r a positive integer). The proof of the main result is based on the framework of Stein’s method. A key contribution is to use a simple generator approximation based on state space collapse.

A famous result in renewal theory is the central limit theorem for renewal processes. Since, in applications, usually only observations from a finite time interval are available, a bound on the Kolmogorov distance to the normal distribution is desirable. We provide an explicit non-uniform bound for the renewal central limit theorem based on Stein’s method and track the explicit values of the constants. For this bound the inter-arrival time distribution is required to have only a second moment. As an intermediate result of independent interest we obtain explicit bounds in a non-central Berry–Esseen theorem under second moment conditions.