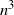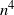1 results
An adjacent-swap Markov chain on coalescent trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 September 2022, pp. 1243-1260
- Print publication:
- December 2022
-
- Article
- Export citation
-
The standard coalescent is widely used in evolutionary biology and population genetics to model the ancestral history of a sample of molecular sequences as a rooted and ranked binary tree. In this paper we present a representation of the space of ranked trees as a space of constrained ordered matched pairs. We use this representation to define ergodic Markov chains on labeled and unlabeled ranked tree shapes analogously to transposition chains on the space of permutations. We show that an adjacent-swap chain on labeled and unlabeled ranked tree shapes has a mixing time at least of order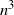
$n^3$
, and at most of order 
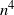$n^{4}$
. Bayesian inference methods rely on Markov chain Monte Carlo methods on the space of trees. Thus it is important to define good Markov chains which are easy to simulate and for which rates of convergence can be studied.
