This dissertation is highly motivated by d.r.e. Nondensity Theorem, which is interesting in two perspectives. One is that it contrasts Sacks Density Theorem, and hence shows that the structures of r.e. degrees and d.r.e. degrees are different. The other is to investigate what other properties a maximal degree can have.

In Chapter 1, we briefly review the backgrounds of Recursion Theory which motivate the topics of this dissertation.

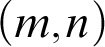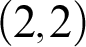In Chapter 2, we introduce the notion of $(m,n)$ -cupping degree. It is closely related to the notion of maximal d.r.e. degree. In fact, a $(2,2)$ -cupping degree is maximal d.r.e. degree. We then prove that there exists an isolated 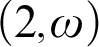$(2,\omega )$ -cupping degree by combining strategies for maximality and isolation with some efforts.

Chapter 3 is part of a joint project with Steffen Lempp, Yiqun Liu, Keng Meng Ng, Cheng Peng, and Guohua Wu. In this chapter, we prove that any finite boolean algebra can be embedded into d.r.e. degrees as a final segment. We examine the proof of d.r.e. Nondensity Theorem and make developments to the technique to make it work for our theorem. The goal of the project is to see what lattice can be embedded into d.r.e. degrees as a final segment, as we observe that the technique has potential be developed further to produce other interesting results.

Abstract prepared by Yong Liu.

E-mail: liuyong0112@nju.edu.cn

In this thesis, we study Turing degrees in the context of classical recursion theory. What we are interested in is the partially ordered structures $\mathcal {D}_{\alpha }$ for ordinals $\alpha <\omega ^2$ and $\mathcal {D}_{a}$ for notations $a\in \mathcal {O}$ with $|a|_{o}\geq \omega ^2$ .

The dissertation is motivated by the $\Sigma _{1}$ -elementary substructure problem: Can one structure in the following structures $\mathcal {R}\subsetneqq \mathcal {D}_{2}\subsetneqq \dots \subsetneqq \mathcal {D}_{\omega }\subsetneqq \mathcal {D}_{\omega +1}\subsetneqq \dots \subsetneqq \mathcal {D(\leq \textbf {0}')}$ be a $\Sigma _{1}$ -elementary substructure of another? For finite levels of the Ershov hierarchy, Cai, Shore, and Slaman [Journal of Mathematical Logic, vol. 12 (2012), p. 1250005] showed that $\mathcal {D}_{n}\npreceq _{1}\mathcal {D}_{m}$ for any $n < m$ . We consider the problem for transfinite levels of the Ershov hierarchy and show that $\mathcal {D}_{\omega }\npreceq _{1}\mathcal {D}_{\omega +1}$ . The techniques in Chapters 2 and 3 are motivated by two remarkable theorems, Sacks Density Theorem and the d.r.e. Nondensity Theorem.

In Chapter 1, we first briefly review the background of the research areas involved in this thesis, and then review some basic definitions and classical theorems. We also summarize our results in Chapter 2 to Chapter 4. In Chapter 2, we show that for any $\omega $ -r.e. set D and r.e. set B with $D<_{T}B$ , there is an $\omega +1$ -r.e. set A such that $D<_{T}A<_{T}B$ . In Chapter 3, we show that for some notation a with $|a|_{o}=\omega ^{2}$ , there is an incomplete $\omega +1$ -r.e. set A such that there are no a-r.e. sets U with $A<_{T}U<_{T}K$ . In Chapter 4, we generalize above results to higher levels (up to $\varepsilon _{0}$ ). We investigate Lachlan sets and minimal degrees on transfinite levels and show that for any notation a, there exists a $\Delta ^{0}_{2}$ -set A such that A is of minimal degree and $A\not \equiv _T U$ for all a-r.e. sets U.

Abstract prepared by Cheng Peng.

E-mail: pengcheng@nankai.edu.cn

Jockusch showed that 2-generic degrees are downward dense below a 2-generic degree. That is, if a is 2-generic, and $0 < {\bf{b}} < {\bf{a}}$, then there is a 2-generic g with $0 < {\bf{g}} < {\bf{b}}.$ In the case of 1-generic degrees Kumabe, and independently Chong and Downey, constructed a minimal degree computable from a 1-generic degree. We explore the tightness of these results.

We solve a question of Barmpalias and Lewis-Pye by constructing a minimal degree computable from a weakly 2-generic one. While there have been full approximation constructions of ${\rm{\Delta }}_3^0$ minimal degrees before, our proof is rather novel since it is a computable full approximation construction where both the generic and the minimal degrees are ${\rm{\Delta }}_3^0 - {\rm{\Delta }}_2^0$.

We show that there is a low T-upper bound for the class of K-trivial sets, namely those which are weak from the point of view of algorithmic randomness. This result is a special case of a more general characterization of ideals in T-degrees for which there is a low T-upper bound.