We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we are concerned with unbounded solutions of the singularly perturbed forced pendulum equation in the presence of friction, namely
Using a limiting energy function, we describe the behaviour of the solutions as the parameter ε approaches zero. We also prove the existence of a family of solutions having a prescribed asymptotic profile and exhibiting a highly rotatory behaviour alternated with a highly oscillatory behaviour in some open subsets of the domain. The proof relies on a combination of the Nehari finite dimensional reduction with the topological degree theory.
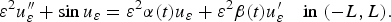$$\varepsilon ^2u_\varepsilon ^{{\prime}{\prime}} + \sin u_\varepsilon = \varepsilon ^2\alpha (t)u_\varepsilon + \varepsilon ^2\beta (t)u_\varepsilon ^{\prime} \quad {\rm in}\;(-L,L).{\rm }$$
