We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let K be a field of characteristic 0, G the direct sum of two copies of the additive group of integers. For a total order ≺ on G, which is compatible with the addition, and for any ċ1, ċ2 ∈ K, we define G-graded highest weight modules M(ċ1, ċ2, ≺) over the Virasoro-like algebra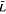 
, indexed by G. It is natural to call them Verma modules. In the present paper, the irreducibility of M (ċ1, ċ2, ≺) is completely determined and the structure of reducible module M (ċ1, ċ2, ≺)is also described.
