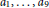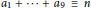Let ${{a}_{1}},\,.\,.\,.\,,\,{{a}_{9}}$ be non-zero integers and $n$ any integer. Suppose that ${{a}_{1}}\,+\,.\,.\,.\,+\,{{a}_{9}}\,\equiv \,n$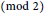$\left( \bmod \,2 \right)$ and 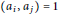$\left( {{a}_{i}},\,{{a}_{i}} \right)\,=\,1$ for 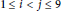$1\,\le \,i\,<\,j\le \,9$. In this paper we prove that

• (i) if 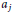${{a}_{j}}$ are not all of the same sign, then the cubic equation 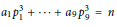${{a}_{1}}p_{1}^{3}\,+\,.\,.\,.\,+\,{{a}_{9}}p_{9}^{3}\,=\,n$ has prime solutions satisfying 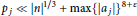${{p}_{j}}\,\ll \,{{\left| n \right|}^{{1}/{3}\;}}\,+\,\max {{\left\{ \left| {{a}_{j}} \right| \right\}}^{8+\varepsilon }}$;

• (ii) if all 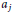${{a}_{j}}$ are positive and 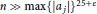$n\,\gg \,\max {{\left\{ \left| {{a}_{j}} \right| \right\}}^{25+\varepsilon }}$ , then 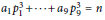${{a}_{1}}p_{1}^{3}\,+\,.\,.\,.\,+\,{{a}_{j}}p_{9}^{3}\,=\,n$ is soluble in primes 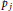$Pj$.

These results improve our previous results with the bounds 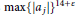$\max {{\left\{ \left| {{a}_{j}} \right| \right\}}^{14+\varepsilon }}$ and 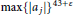$\max \,{{\left\{ \left| {{a}_{j}} \right| \right\}}^{43+\varepsilon }}$ in place of 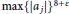$\max {{\left\{ \left| {{a}_{j}} \right| \right\}}^{8+\varepsilon }}$ and 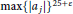$\max {{\left\{ \left| {{a}_{j}} \right| \right\}}^{25+\varepsilon }}$ above, respectively.

It is shown that every sufficiently large integer congruent to $14$ modulo $240$ may be written as the sum of $14$ fourth powers of prime numbers, and that every sufficiently large odd integer may be written as the sum of $21$ fifth powers of prime numbers. The respective implicit bounds $14$ and $21$ improve on the previous bounds $15$ (following from work of Davenport) and $23$ (due to Thanigasalam). These conclusions are established through the medium of the Hardy-Littlewood method, the proofs being somewhat novel in their use of estimates stemming directly from exponential sums over prime numbers in combination with the linear sieve, rather than the conventional methods which `waste' a variable or two by throwing minor arc estimates down to an auxiliary mean value estimate based on variables not restricted to be prime numbers. In the work on fifth powers, a switching principle is applied to a cognate problem involving almost primes in order to obtain the desired conclusion involving prime numbers alone. 2000 Mathematics Subject Classification: 11P05, 11N36, 11L15, 11P55.