Weighted Logic is a powerful tool for the specification of calculations over semirings that depend on qualitative information. Using a novel combination of Weighted Logic and Here-and-There (HT) Logic, in which this dependence is based on intuitionistic grounds, we introduce Answer Set Programming with Algebraic Constraints (ASP(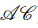 $\mathcal A \mathcal C$)), where rules may contain constraints that compare semiring values to weighted formula evaluations. Such constraints provide streamlined access to a manifold of constructs available in ASP, like aggregates, choice constraints, and arithmetic operators. They extend some of them and provide a generic framework for defining programs with algebraic computation, which can be fruitfully used e.g. for provenance semantics of datalog programs. While undecidable in general, expressive fragments of ASP(
$\mathcal A \mathcal C$)), where rules may contain constraints that compare semiring values to weighted formula evaluations. Such constraints provide streamlined access to a manifold of constructs available in ASP, like aggregates, choice constraints, and arithmetic operators. They extend some of them and provide a generic framework for defining programs with algebraic computation, which can be fruitfully used e.g. for provenance semantics of datalog programs. While undecidable in general, expressive fragments of ASP(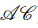 $\mathcal A \mathcal C$) can be exploited for effective problem solving in a rich framework.
$\mathcal A \mathcal C$) can be exploited for effective problem solving in a rich framework.
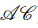 $\mathcal A \mathcal C$): Answer Set Programming with Algebraic Constraints
$\mathcal A \mathcal C$): Answer Set Programming with Algebraic Constraints