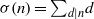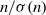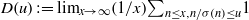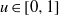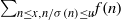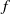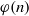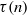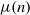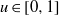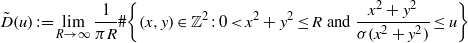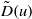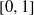1 results
VARIATIONS ON A THEOREM OF DAVENPORT CONCERNING ABUNDANT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 12 September 2013, pp. 437-450
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
-
Let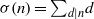
$\sigma (n)= {\mathop{\sum }\nolimits}_{d\mid n} d$ be the usual sum-of-divisors function. In 1933, Davenport showed that 
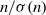$n/ \sigma (n)$ possesses a continuous distribution function. In other words, the limit 
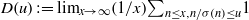$D(u): = \lim _{x\rightarrow \infty }(1/ x){\mathop{\sum }\nolimits}_{n\leq x, n/ \sigma (n)\leq u} 1$ exists for all 
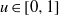$u\in [0, 1] $ and varies continuously with 
$u$. We study the behaviour of the sums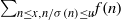 
${\mathop{\sum }\nolimits}_{n\leq x, n/ \sigma (n)\leq u} f(n)$ for certain complex-valued multiplicative functions 
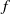$f$. Our results cover many of the more frequently encountered functions, including 
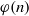$\varphi (n)$, 
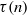$\tau (n)$ and 
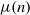$\mu (n)$. They also apply to the representation function for sums of two squares, yielding the following analogue of Davenport’s result: for all 
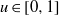$u\in [0, 1] $, the limit exists, and
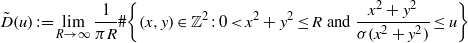$$\begin{eqnarray*}\tilde {D} (u): = \lim _{R\rightarrow \infty }\frac{1}{\pi R} \# \biggl\{ (x, y)\in { \mathbb{Z} }^{2} : 0\lt {x}^{2} + {y}^{2} \leq R\text{ and } \frac{{x}^{2} + {y}^{2} }{\sigma ({x}^{2} + {y}^{2} )} \leq u\biggr\}\end{eqnarray*}$$
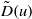$\tilde {D} (u)$ is both continuous and strictly increasing on 
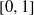$[0, 1] $.
