Graph-based causal models are a flexible tool for causal inference from observational data. In this paper, we develop a comprehensive framework to define, identify, and estimate a broad class of causal quantities in linearly parametrized graph-based models. The proposed method extends the literature, which mainly focuses on causal effects on the mean level and the variance of an outcome variable. For example, we show how to compute the probability that an outcome variable realizes within a target range of values given an intervention, a causal quantity we refer to as the probability of treatment success. We link graph-based causal quantities defined via the do-operator to parameters of the model implied distribution of the observed variables using so-called causal effect functions. Based on these causal effect functions, we propose estimators for causal quantities and show that these estimators are consistent and converge at a rate of \documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$N^{-1/2}$$\end{document}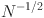 under standard assumptions. Thus, causal quantities can be estimated based on sample sizes that are typically available in the social and behavioral sciences. In case of maximum likelihood estimation, the estimators are asymptotically efficient. We illustrate the proposed method with an example based on empirical data, placing special emphasis on the difference between the interventional and conditional distribution.
under standard assumptions. Thus, causal quantities can be estimated based on sample sizes that are typically available in the social and behavioral sciences. In case of maximum likelihood estimation, the estimators are asymptotically efficient. We illustrate the proposed method with an example based on empirical data, placing special emphasis on the difference between the interventional and conditional distribution.