We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let P be a closed convex cone in 
$\mathbb{R}^d$ which is assumed to be spanning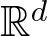 
$\mathbb{R}^d$ and contains no line. In this article, we consider a family of CAR flows over P and study the decomposability of the associated product systems. We establish a necessary and sufficient condition for CAR flow to be decomposable. As a consequence, we show that there are uncountable many CAR flows which are cocycle conjugate to the corresponding CCR flows.
