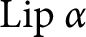1 results
Approximation via Hausdorff operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2020, pp. 512-529
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
-
Truncating the Fourier transform averaged by means of a generalized Hausdorff operator, we approximate functions and the adjoint to that Hausdorff operator of the given function. We find estimates for the rate of approximation in various metrics in terms of the parameter of truncation and the components of the Hausdorff operator. Explicit rates of approximation of functions and comparison with approximate identities are given in the case of continuous functions from the class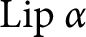
$\text {Lip }\alpha $
.
