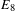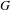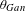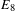Refine search
Actions for selected content:
1 results
THE MINIMAL MODULAR FORM ON QUATERNIONIC
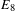 $E_{8}$
$E_{8}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 20 August 2020, pp. 603-636
- Print publication:
- March 2022
-
- Article
- Export citation