In a recent paper, motivated by the study of central extensions of associative algebras, George Janelidze introduces the notion of weakly action representable category. In this paper, we show that the category of Leibniz algebras is weakly action representable and we characterize the class of acting morphisms. Moreover, we study the representability of actions of the category of Poisson algebras and we prove that the subvariety of commutative Poisson algebras is not weakly action representable.

We generate an algebra on blood phenotypes with multiplication based on the human ABO-blood group inheritance pattern. We assume that gametes are not chosen randomly during meiosis. We investigate some of the properties of this algebra, namely, the set of idempotents, lattice of ideals and the associative enveloping algebra.

We describe all finite dimensional uniserial representations of a commutative associative (resp. abelian Lie) algebra over a perfect (resp. sufficiently large perfect) field. In the Lie case the size of the field depends on the answer to following question, considered and solved in this paper. Let 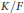$K/F$ be a finite separable field extension and let 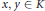$x,\,y\,\in \,K$. When is $F\left[ x,\,y \right]\,=\,F\left[ \alpha x\,+\,\beta y \right]$ for some nonzero elements 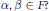$\alpha ,\,\beta \,\in \,F?$

This paper is devoted to the complete classification of integrable one-component evolution equations whose field variable takes its values in an associative algebra. The proof that the list of non-commutative integrable homogeneous evolution equations is complete relies on the symbolic method. Each equation in the list has infinitely many local symmetries and these can be generated by its recursion (recursive) operator or master symmetry. 1991 Mathematics Subject Classification: 13A50, 16-XX, 22E70, 35A30, 35Q53, 58F07.