We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the semilinear Schrödinger equation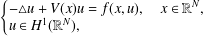 where 
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}-\triangle u+V(x)u=f(x,u),\quad x\in \mathbb{R}^{N},\\ u\in H^{1}(\mathbb{R}^{N}),\end{array}\right.\end{eqnarray}$$
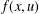$f(x,u)$ is asymptotically linear with respect to 
$u$,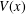 
$V(x)$ is 1-periodic in each of 
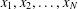$x_{1},x_{2},\dots ,x_{N}$ and 
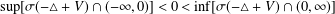$\sup [{\it\sigma}(-\triangle +V)\cap (-\infty ,0)]<0<\inf [{\it\sigma}(-\triangle +V)\cap (0,\infty )]$. We develop a direct approach to find ground state solutions of Nehari–Pankov type for the above problem. The main idea is to find a minimizing Cerami sequence for the energy functional outside the Nehari–Pankov manifold 
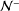${\mathcal{N}}^{-}$ by using the diagonal method.
