1 results
Residues of Eisenstein series and the automorphic cohomology of reductive groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 7 / July 2013
- Published online by Cambridge University Press:
- 07 May 2013, pp. 1061-1090
- Print publication:
- July 2013
-
- Article
-
- You have access
- Export citation
-
Let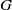
$G$ be a connected, reductive algebraic group over a number field 
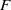$F$ and let 
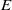$E$ be an algebraic representation of 
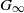${G}_{\infty } $. In this paper we describe the Eisenstein cohomology 
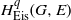${ H}_{\mathrm{Eis} }^{q} (G, E)$ of 
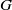$G$ below a certain degree 
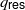${q}_{ \mathsf{res} } $ in terms of Franke’s filtration of the space of automorphic forms. This entails a description of the map 
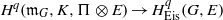${H}^{q} ({\mathfrak{m}}_{G} , K, \Pi \otimes E)\rightarrow { H}_{\mathrm{Eis} }^{q} (G, E)$, 
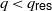$q\lt {q}_{ \mathsf{res} } $, for all automorphic representations 
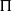$\Pi $ of 
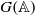$G( \mathbb{A} )$ appearing in the residual spectrum. Moreover, we show that below an easily computable degree 
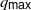${q}_{ \mathsf{max} } $, the space of Eisenstein cohomology 
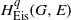${ H}_{\mathrm{Eis} }^{q} (G, E)$ is isomorphic to the cohomology of the space of square-integrable, residual automorphic forms. We discuss some more consequences of our result and apply it, in order to derive a result on the residual Eisenstein cohomology of inner forms of 
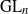${\mathrm{GL} }_{n} $ and the split classical groups of type 
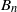${B}_{n} $, 
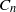${C}_{n} $, 
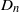${D}_{n} $.
