1 results
Metric Spaces Admitting Low-distortion Embeddings into All n-dimensional Banach Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 4 / 01 August 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 876-907
- Print publication:
- 01 August 2016
-
- Article
-
- You have access
- Export citation
-
For a fixed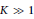
$K\,\gg \,1$ and 
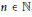$n\,\in \,\mathbb{N}$, 
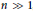$n\,\gg \,1$ we study metric spaces which admit embeddings with distortion 
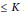$\le \,K$ into each 
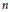$n$-dimensional Banach space. Classical examples include spaces embeddable into log 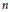$n$-dimensional Euclidean spaces, and equilateral spaces.We prove that good embeddability properties are preserved under the operation of metric composition of metric spaces. In particular, we prove that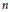
$n$-point ultrametrics can be embedded with uniformly bounded distortions into arbitrary Banach spaces of dimension 
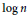$\log \,n$.The main result of the paper is a new example of a family of finite metric spaces which are not metric compositions of classical examples and which do embed with uniformly bounded distortion into any Banach space of dimension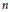
$n$. This partially answers a question of G. Schechtman.
