This paper answers a recent question concerning the relationship between two notions of paracompactness for bitopological spaces. Romaguera and Marin defined pairwise paracompactness in terms of pair open covers, motivated by a characterization of paracompactness due to Junnila. On the other hand, Raghavan and Reilly defined a bitopological space (X, τ, σ) to be δ-pairwise paracompact if and only if every τ open (σ open) cover of X admits a τ V σ open refinement which is τ V σ locally finite. It is shown that pairwise paracompactness implies δ-pairwise paracompactness, and that the converse is false.

In this paper we prove that a pairwise Hausdorff bitopological space 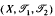is quasi-metrizable if and only if for each point x ∈ X and for i, j = 1,2, i ≠ j, one can assign 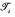nbd bases { S(n, i; x) | n = 1, 2,… } such that (i) y ∉ S (n − 1, i; x) imples S(n, i; x) ∩ S (n, j; y) = φ, (ii) y ∈ S (n, i; x) implies S (n, i; y) ⊂ S(n − 1, i; x). We derive two further results from this.

Based on a Junnila's paracompactness characterization we give a definition of pairwise paracompact space which permits us to prove that a bitopological space is quasi-metrizable if, and only if, it is a pairwise developable and pairwise paracompact space. An easy consequence of this result is the biquasi-metric form of the Morita metrization theorem. We also give some results on open mappings and strong quasi-metrics.