A numerical study of the saturation process inside a rectangular open cavity is presented. Previous experiments and linear stability analysis of the problem completely described the flow in its onset, as well as in a saturated regime, characterized by three-dimensional centrifugal modes. The morphology of the modes found in the experiments matched the ones predicted by linear analysis, but with a shift in frequencies for the oscillating modes. A three-dimensional incompressible direct numerical simulation (DNS) is employed for a detailed investigation of the saturation process inside a cavity with dimensions similar to the one used in the experiments, to further explain the behaviour of these modes. In this work, periodic boundary conditions are first imposed to better understand the effect of the saturation process far from the walls. Then, the effects of spanwise solid wall boundary conditions are investigated with a DNS reproducing the full dynamics of the experiments. The main flow structures are identified using the dynamic mode decomposition technique and compared with previous experimental and linear stability analysis results. The main reason for the aforementioned shift in frequency is explained in this paper, as it is a function of the velocity of the main recirculating vortex.

In this paper, an alternative lattice Boltzmann (LB)model for incompressible flows is proposed. By modifying directly the moments of the equilibrium distribution function (EDF), the continuous expression of the EDF in tensor Hermite polynomials is derived using the moment expansion and then discretizedwith the discrete velocity vectors of the D2Q9 lattice. The present model as well as its counterpart, the incompressible LB model proposed by Guo, reproduces the incompressible Navier-Stokes (N-S) equations for both steady and unsteady flows. Besides, an alternative pressure formula, which represents the pressure as the diagonal part of the stress tensor, is adopted in the present model. Furthermore, in order to enhance the stability of the present LB model, an additional relaxation time pertaining to the non-hydrodynamic mode is added to the BGK collision operator. The present LB model is validated by two benchmark tests: the cavity flow with different Reynolds number (Re) and the flow past an impulsively started cylinder at Re=40 and 550.

Three-dimensional instabilities arising in open cavity flows are responsible for complex broad-banded dynamics. Existing studies either focus on theoretical properties of ideal simplified flows or observe the final state of experimental flows. This paper aims to establish a connection between the onset of the centrifugal instabilities and their final expression within the fully saturated flow. To that end, a linear three-dimensional modal instability analysis of steady two-dimensional states developing in an open cavity of aspect ratio $L/D=2$ (length over depth) is conducted. This analysis is performed together with an experimental study in the same geometry adding spanwise endwalls. Two different Reynolds numbers are investigated through spectral analyses and modal decomposition. The physics of the flow is thoroughly described exploiting the strengths of each methodology. The main flow structures are identified and salient space and time scales are characterised. Results indicate that the structures obtained from linear analysis are mainly consistent with the fully saturated experimental flow. The analysis also brings to light the selection and alteration of certain wave properties, which could be caused by nonlinearities or the change of spanwise boundary conditions.

We perform a global stability analysis of a flow over an open cavity, characterized by a Reynolds number, based on the upstream velocity and the cavity length, of 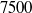$7500$. We compute base flows and unstable global modes of the flow for different Mach numbers ranging from 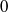$0$ to 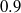$0. 9$. In the incompressible regime (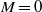$M= 0$), we show that the flow is subject to global instabilities due to Kelvin–Helmholtz instabilities in the shear layer, which become strengthened by a hydrodynamic pressure feedback. The influence of the boundary-layer thickness and of the length-to-depth ratio of the cavity on these shear-layer modes has been investigated. In the compressible regime (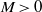$M\gt 0$), we have shown that all unstable global modes are continuously connected to the incompressible shear-layer modes as 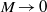$M\rightarrow 0$. These shear-layer modes correspond to the beginning of branches of global modes, whose frequencies evolve (as a function of the Mach number), in accordance with the feedback aeroacoustic mechanism (Rossiter, Tech. Rep. Aero. Res. Counc. R. & M., 1964). We have also identified branches of global modes behaving in agreement with acoustic resonance mechanisms (East, J. Sound Vib., vol. 3, 1966, pp. 277–287; Tam, J. Sound Vib., vol. 49, 1976, pp. 353–364; Koch, AIAA J., vol. 43, 2005, pp. 2342–2349). At the intersections between both types of branches, the growth rate of the global modes is seen to display a local maximum. Along the aeroacoustic feedback branches, the number of vortical structures in the shear layer is kept constant, while the pressure pattern inside the cavity is conserved along the acoustic resonance branches. We show that both the feedback aeroacoustic and acoustic resonance mechanisms are at play over the entire subsonic regime, from 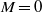$M= 0$ to 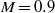$M= 0. 9$. At low Mach numbers, we suggest that it is still the feedback aeroacoustic mechanism that selects the frequency, even though the fundamental acoustic resonance mode is also important due to enhancing the response. At higher Mach numbers, we observe that the pressure pattern of the acoustic resonance modes (fundamental acoustic modes, first longitudinal acoustic modes, first longitudinal-depth acoustic modes) inside the cavity determines the directivity of the radiated noise. Links with experimental results are finally discussed.