In this note, we exhibit concrete examples of characterizing slopes for the knot 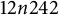 $12n242$, also known as the
$12n242$, also known as the 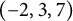 $(-2,3,7)$-pretzel knot. Although it was shown by Lackenby that every knot admits infinitely many characterizing slopes, the nonconstructive nature of the proof means that there are very few hyperbolic knots for which explicit examples of characterizing slopes are known.
$(-2,3,7)$-pretzel knot. Although it was shown by Lackenby that every knot admits infinitely many characterizing slopes, the nonconstructive nature of the proof means that there are very few hyperbolic knots for which explicit examples of characterizing slopes are known.
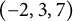 $(-2,3,7)$-pretzel knot
$(-2,3,7)$-pretzel knot