1 results
Equivariant Formality for Actions of Torus Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 6 / 01 December 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1290-1307
- Print publication:
- 01 December 2004
-
- Article
-
- You have access
- Export citation
-
This paper contains a comparison of several definitions of equivariant formality for actions of torus groups. We develop and prove some relations between the definitions. Focusing on the case of the circle group, we use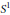
${{S}^{1}}$
-equivariant minimal models to give a number of examples of 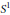${{S}^{1}}$-spaces illustrating the properties of the various definitions.
