We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The coincidence degree for the pair (L, N) developed by Mawhin (1972) provides a method for proving the existence of solutions of the equation Lx = Nx where L: dom L ⊂ X → Z is a linear Fredholm mapping of index zero and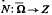 
is a (possiblv nonlinear) mapping and Ω is a bounded open subset of X, X and Z being normed linear spaces over the reals. In this paper we have extended the coincidence degree for the pair (L, N) to solve the equation 
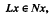, where L: dom L ⊂ X → Z is a linear Fredholm mapping of index zero, 
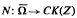and X, Z and Ω are as above, CK(Z) being the set of compact convex subsets of Z.
Subject classification (Amer. Math. Soc. (MOS) 1970): primary 47 H 15, 47 A 50; secondary 47 H 10, 47 A 55.
