We study lens space surgeries along two different families of 2-component links, denoted by 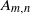 ${A}_{m, n} $ and
${A}_{m, n} $ and 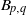 ${B}_{p, q} $, related with the rational homology
${B}_{p, q} $, related with the rational homology 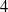 $4$-ball used in J. Park’s (generalized) rational blow down. We determine which coefficient
$4$-ball used in J. Park’s (generalized) rational blow down. We determine which coefficient  $r$ of the knotted component of the link yields a lens space by Dehn surgery. The link
$r$ of the knotted component of the link yields a lens space by Dehn surgery. The link 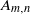 ${A}_{m, n} $ yields a lens space only by the known surgery with
${A}_{m, n} $ yields a lens space only by the known surgery with  $r= mn$ and unexpectedly with
$r= mn$ and unexpectedly with 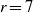 $r= 7$ for
$r= 7$ for 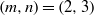 $(m, n)= (2, 3)$. On the other hand,
$(m, n)= (2, 3)$. On the other hand, 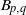 ${B}_{p, q} $ yields a lens space by infinitely many
${B}_{p, q} $ yields a lens space by infinitely many  $r$. Our main tool for the proof are the Reidemeister-Turaev torsions, that is, Reidemeister torsions with combinatorial Euler structures. Our results can be extended to the links whose Alexander polynomials are same as those of
$r$. Our main tool for the proof are the Reidemeister-Turaev torsions, that is, Reidemeister torsions with combinatorial Euler structures. Our results can be extended to the links whose Alexander polynomials are same as those of 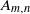 ${A}_{m, n} $ and
${A}_{m, n} $ and 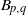 ${B}_{p, q} $.
${B}_{p, q} $.