Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

2 results

  • The Euler characteristic and Euler defect for comodules over Euler coalgebras

  • Daniel Simson
  • Journal:
    Journal of K-Theory / Volume 7 / Issue 1 / February 2011
    Published online by Cambridge University Press:
    13 November 2009, pp. 91-113
    Print publication:
    February 2011

  • Let K be a field. We study a class of left C-comodules over a basic left Euler coalgebra C by means of the Euler ℤ-bilinear form 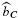associated to C, the Euler characteristic χC(M,N) of left C-comodules M,N, and the defect ∂C(M,N) ∊ ℤ associated to any computable Euler pair (M,N) of left C-comodules. We show that 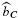(lgthM, lgthN) = χC(M,N) + ∂C(M,N), for any computable Euler pair (M,N) of comodules over a left Euler coalgebra C. One of the main results of the paper asserts that the defect ∂C(M,N) is zero and 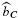(lgthM,lgthN) = χC(M,N), if the comodules M,N are finite-dimensional.

  • Local cohomology of ${BP_{*}BP}$-comodules

  • Mark Hovey, Neil Strickland
  • Journal:
    Proceedings of the London Mathematical Society / Volume 90 / Issue 2 / March 2005
    Published online by Cambridge University Press:
    25 February 2005, pp. 521-544
    Print publication:
    March 2005

  • Given a spectrum $X$, we construct a spectral sequence of $BP_{*}BP$-comodules that converges to $BP_{*}(L_{n}X)$, where $L_{n}X$ is the Bousfield localization of $X$ with respect to the Johnson–Wilson theory $E(n)_{*}$. The $E_{2}$-term of this spectral sequence consists of the derived functors of an algebraic version of $L_{n}$. We show how to calculate these derived functors, which are closely related to local cohomology of $BP_{*}$-modules with respect to the ideal $I_{n + 1}$.