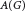We construct and examine an operator space $X$, isometric to $\ell_2$, such that every completely bounded map from its subspace $Y$ into $X$ is a compact perturbation of a linear combination of multiples of a shift of given multiplicity and their adjoints. Moreover, every completely bounded map on $X$ is a Hilbert–Schmidt perturbation of such a linear combination.

We introduce and investigate using Hilbert modules the properties of the Fourier algebra$A(G)$ for a locally compact groupoid $G$. We establish a duality theorem for such groupoids in terms of multiplicative module maps. This includes as a special case the classical duality theorem for locally compact groups proved by P. Eymard.

We solve a joint similarity problem for pairs of operators of Foias–Williams/Peller type on weighted Bergman spaces. We show that for the single operator, the Hardy space theory established by Bourgain and Aleksandrov–Peller carries over to weighted Bergman spaces, by establishing the relevant weak factorizations. We then use this fact, together with a recent dilation result due to the first author and Rochberg, to show that a commuting pair of such operators is jointly polynomially bounded if and only if it is jointly completely polynomially bounded. In this case, the pair is jointly similar to a pair of contractions by Paulsen’s similarity theorem.

AMS 2000 Mathematics subject classification: Primary 47B35; 47B47