We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we study real hypersurfaces in a non-flat complex space form with 
$\eta $-parallel shape operator. Several partial characterizations of these real hypersurfaces are obtained.
Real hypersurfaces in a complex space form whose structure Jacobi operator is symmetric along the Reeb flow are studied. Among them, homogeneous real hypersurfaces of type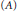 
$\left( A \right)$ in a complex projective or hyperbolic space are characterized as those whose structure Jacobi operator commutes with the shape operator.
