We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider a piecewise-deterministic Markov process (Xt) governed by a jump intensity function, a rate function that determines the behaviour between jumps, and a stochastic kernel describing the conditional distribution of jump sizes. The paper deals with the point process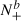 
of upcrossings of some level b by (Xt). We prove a version of Rice's formula relating the stationary density of (Xt) to level crossing intensities and show that, for a wide class of processes (Xt), as b → ∞, the scaled point process 
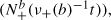where ν+(b) denotes the intensity of upcrossings of b, converges weakly to a geometrically compound Poisson process.
